TD3 - Compression Shannon-Huffman¶
A. The goal of this part is to implement the Huffman coding and how it can be enhanced to reach the optimal bound.¶
from __future__ import division
import numpy as np
import scipy as sp
import pylab as pl
import scipy.signal as sg
import matplotlib.pyplot as plt
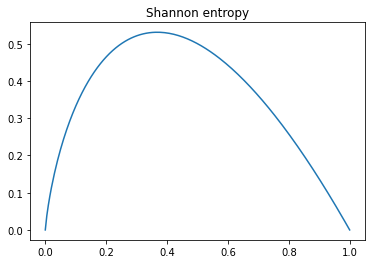
The definition of the entropy: Given a probability vector on a finite space \(\Omega = \{\omega_1,\ldots,\omega_n\}\) denoted by \(p = (p_1,\ldots,p_n)\). The entropy is the quantity defined by \(H(p) = -\sum_{i = 1}^n p_i \log(p_i)\). It’s a concave function which is positive since \(p_i \in [0,1]\) and thus \(\log(p_i) \leq 0\).¶
def ShannonEntropy(p):
return -np.sum(p*np.log2(np.maximum(p,1e-15)))
n = 200
x = np.linspace(1e-10,1,n)
plt.title("Shannon entropy")
plt.plot(x,-x*np.log2(x))
[<matplotlib.lines.Line2D at 0x7f12838bc450>]
In what follows, we consider that the \(\omega_i\) are letters of some alphabet which have a frequency of appearance of \(p_i\).¶
## Generate a random text according to the frequencies.
n = 512
p = 0.3
x = (np.random.rand(n) > p) + 1
h = [np.sum(x == 1), np.sum(x == 2)]
h = h/np.sum(h)
print(f"probability distribution : {h}")
print(f"Theoretical probability : {p}")
print(f"Empirical probability : {h[0]}")
probability distribution : [0.296875 0.703125]
Theoretical probability : 0.3
Empirical probability : 0.296875
e = ShannonEntropy(h)
print("Entropy = %.2f" %e)
Entropy = 0.88
### Definition of the probability h
h = [.1, .15, .4, .15, .2]
print(f"Entropy = {ShannonEntropy(h)}")
Entropy = 2.1464393446710153
We use a python library to represent a binary tree. We assume that the tree is coded in the following way, here is an example, \((a,((b,c),(d,e))\).¶
import igraph as ig # also needs 'pip install pycairo'
# https://igraph.org/python/doc/tutorial/tutorial.html#layouts-and-plotting
g = ig.Graph()
g.add_vertices(8)
g.vs["name"] = ["A", " ", " ", " ", "B", "D", "E", "C"]
g.add_edges([(0,1), (1,2), (1, 3), (3, 5), (3, 6), (2, 7), (2, 4)])
# Display the graph
visual_style = {}
visual_style["bbox"] = (300, 300)
visual_style["vertex_label"] = g.vs["name"]
ig.plot(g, layout = g.layout_reingold_tilford(root=[0]), **visual_style)
Q1. Write a function that generates the Huffman tree with the probability \(h\) as input. Plot the tree with the function above.¶
## Create the tree as a list.
# https://www.math.upenn.edu/~deturck/m170/wk8/lecture/huffman/huffman.html
# https://bhrigu.me/blog/2017/01/17/huffman-coding-python-implementation/
class NodeTree(object):
def __init__(self, name, proba, left=None, right=None):
self.name = name
self.proba = proba
self.left = left
self.right = right
# h a vector of proba
def CreateTree(h):
nodes = [NodeTree(chr(65 + idx), proba) for idx, proba in enumerate(h)]
nodes = sorted(nodes, key=lambda node: node.proba, reverse=True)
while (len(nodes) > 1):
left = nodes.pop()
right = nodes.pop()
node = NodeTree('', left.proba + right.proba, left, right)
nodes.append(node)
nodes = sorted(nodes, key=lambda node: node.proba, reverse=True)
return nodes[0]
# root a NodeTree root node
def BuildIgGraph(root):
g = ig.Graph()
queue = []
rootIdx = g.add_vertex((root.name, root.proba)).index
queue.append([root, rootIdx])
while len(queue):
[root, idx] = queue.pop()
[left, right] = [root.left, root.right]
if left:
leftIdx = g.add_vertex((left.name, left.proba)).index
g.add_edge(idx, leftIdx)
queue.append([left, leftIdx])
if right:
rightIdx = g.add_vertex((right.name, right.proba)).index
g.add_edge(idx, rightIdx)
queue.append([right, rightIdx])
return g
def print2DUtil(root, space = 0):
if (root == None):
return
space += 10
print2DUtil(root.right, space)
# Print current node after space
print()
for i in range(10, space):
print(end = " ")
print(root.name + " (" + str(root.proba) + ")")
# Process left child
print2DUtil(root.left, space)
root = CreateTree(h)
g = BuildIgGraph(root)
ig.plot(g, layout = g.layout_reingold_tilford(root=0), vertex_label_dist = -1, vertex_label=g.vs["name"], bbox = (500, 300))
#print2DUtil(root)
Q2. Write the function HuffmanGencode which computes the Huffman code of an element in \(0,1,2,3,4\) and print it.¶
def getPathFromX(root, path, x):
if (not root):
return False
# if it is the required node
# return true
if (root.name == x):
return True
# else check whether the required node
# lies in the left subtree or right
# subtree of the current node
if getPathFromX(root.left, path, x):
path.append(0)
return True
if getPathFromX(root.right, path, x):
path.append(1)
return True
# required node does not lie either in
# the left or right subtree of the current
# node. Thus, remove current node's value
# from 'arr'and then return false
if (len(path) > 1):
path.pop(-1)
def HuffmanGencode(root, letter):
keys = [chr(65 + c) for c in range(0, letter)] # Alphabet until letter
codes = {}
for i, key in enumerate(keys):
path = []
getPathFromX(root, path, key)
pathChain = ''
for d in path:
pathChain += str(d)
#don't forget to reverse the path because the tree is traversed in reverse
pathChain = pathChain[::-1]
codes.update({keys[i]:pathChain})
return codes
# vector to store the path
codes = HuffmanGencode(root, 5)
print("A == 0, B == 1, etc")
print(codes)
A == 0, B == 1, etc
{'A': '100', 'B': '110', 'C': '0', 'D': '101', 'E': '111'}
Q3. Write a function that generates a random sequence of numbers between \(0\) and \(4\) according to the probability \(h\).¶
from numpy import random
def RandGen(p, number):
return random.choice([0,1,2,3,4], p=p, size=(number))
message = RandGen(h, 512) # 0 is for 'A' and so on
print(message)
print("-----------------")
print("TO LETTER !")
print("-----------------")
print([chr(65 + m) for m in message])
[2 2 3 3 1 2 2 2 2 4 0 4 2 3 2 4 4 2 2 4 0 0 1 2 2 2 2 3 0 0 1 4 2 1 3 3 0
2 1 2 1 2 1 2 2 2 1 1 2 3 1 4 2 4 2 4 1 2 3 1 2 1 2 1 0 2 2 3 4 4 1 0 3 0
3 3 2 0 3 4 3 4 2 2 4 0 1 2 4 2 4 2 2 3 3 3 2 2 2 2 3 4 2 3 2 0 3 2 4 2 2
1 0 0 2 2 3 2 2 4 2 3 2 2 2 4 0 2 2 2 2 4 2 2 3 2 1 4 2 3 2 3 4 0 1 2 0 2
1 3 3 3 4 3 2 2 2 1 1 2 1 4 4 2 2 1 3 4 2 0 1 3 4 2 4 1 0 4 0 1 0 2 2 0 2
2 1 2 2 2 4 2 0 4 0 2 2 3 1 2 3 4 2 2 2 3 2 2 2 2 3 3 2 0 2 4 1 2 0 3 4 1
4 2 1 2 3 2 4 2 2 1 0 2 4 2 4 0 2 2 3 1 4 1 2 2 3 2 4 1 4 1 4 2 2 4 3 3 2
3 2 3 2 4 2 4 2 0 2 2 2 1 0 2 4 2 2 4 1 2 2 2 4 4 2 4 2 4 3 0 2 4 1 2 4 0
1 2 1 2 0 4 2 4 2 3 2 3 0 1 4 4 0 1 2 4 3 2 1 2 4 3 3 4 0 2 2 2 0 4 2 3 2
4 3 0 1 0 0 3 2 2 2 1 2 0 2 2 0 2 0 4 2 4 2 0 0 3 4 2 2 2 4 2 2 2 0 2 3 4
2 2 3 1 2 4 4 2 0 3 3 2 2 0 2 2 2 3 2 3 3 2 2 2 1 2 1 4 2 2 1 4 4 2 4 2 4
2 2 0 4 2 0 4 3 1 3 2 4 2 4 4 4 0 2 3 2 2 2 2 0 2 2 3 4 2 3 4 3 4 4 4 2 4
1 4 2 1 3 1 4 4 2 1 2 0 3 4 2 0 0 3 2 4 2 4 1 4 2 0 1 4 0 2 0 1 2 2 3 4 4
2 3 2 4 3 2 0 2 4 4 3 4 2 1 2 2 2 1 1 2 4 2 3 4 3 4 1 1 2 4 2]
-----------------
TO LETTER !
-----------------
['C', 'C', 'D', 'D', 'B', 'C', 'C', 'C', 'C', 'E', 'A', 'E', 'C', 'D', 'C', 'E', 'E', 'C', 'C', 'E', 'A', 'A', 'B', 'C', 'C', 'C', 'C', 'D', 'A', 'A', 'B', 'E', 'C', 'B', 'D', 'D', 'A', 'C', 'B', 'C', 'B', 'C', 'B', 'C', 'C', 'C', 'B', 'B', 'C', 'D', 'B', 'E', 'C', 'E', 'C', 'E', 'B', 'C', 'D', 'B', 'C', 'B', 'C', 'B', 'A', 'C', 'C', 'D', 'E', 'E', 'B', 'A', 'D', 'A', 'D', 'D', 'C', 'A', 'D', 'E', 'D', 'E', 'C', 'C', 'E', 'A', 'B', 'C', 'E', 'C', 'E', 'C', 'C', 'D', 'D', 'D', 'C', 'C', 'C', 'C', 'D', 'E', 'C', 'D', 'C', 'A', 'D', 'C', 'E', 'C', 'C', 'B', 'A', 'A', 'C', 'C', 'D', 'C', 'C', 'E', 'C', 'D', 'C', 'C', 'C', 'E', 'A', 'C', 'C', 'C', 'C', 'E', 'C', 'C', 'D', 'C', 'B', 'E', 'C', 'D', 'C', 'D', 'E', 'A', 'B', 'C', 'A', 'C', 'B', 'D', 'D', 'D', 'E', 'D', 'C', 'C', 'C', 'B', 'B', 'C', 'B', 'E', 'E', 'C', 'C', 'B', 'D', 'E', 'C', 'A', 'B', 'D', 'E', 'C', 'E', 'B', 'A', 'E', 'A', 'B', 'A', 'C', 'C', 'A', 'C', 'C', 'B', 'C', 'C', 'C', 'E', 'C', 'A', 'E', 'A', 'C', 'C', 'D', 'B', 'C', 'D', 'E', 'C', 'C', 'C', 'D', 'C', 'C', 'C', 'C', 'D', 'D', 'C', 'A', 'C', 'E', 'B', 'C', 'A', 'D', 'E', 'B', 'E', 'C', 'B', 'C', 'D', 'C', 'E', 'C', 'C', 'B', 'A', 'C', 'E', 'C', 'E', 'A', 'C', 'C', 'D', 'B', 'E', 'B', 'C', 'C', 'D', 'C', 'E', 'B', 'E', 'B', 'E', 'C', 'C', 'E', 'D', 'D', 'C', 'D', 'C', 'D', 'C', 'E', 'C', 'E', 'C', 'A', 'C', 'C', 'C', 'B', 'A', 'C', 'E', 'C', 'C', 'E', 'B', 'C', 'C', 'C', 'E', 'E', 'C', 'E', 'C', 'E', 'D', 'A', 'C', 'E', 'B', 'C', 'E', 'A', 'B', 'C', 'B', 'C', 'A', 'E', 'C', 'E', 'C', 'D', 'C', 'D', 'A', 'B', 'E', 'E', 'A', 'B', 'C', 'E', 'D', 'C', 'B', 'C', 'E', 'D', 'D', 'E', 'A', 'C', 'C', 'C', 'A', 'E', 'C', 'D', 'C', 'E', 'D', 'A', 'B', 'A', 'A', 'D', 'C', 'C', 'C', 'B', 'C', 'A', 'C', 'C', 'A', 'C', 'A', 'E', 'C', 'E', 'C', 'A', 'A', 'D', 'E', 'C', 'C', 'C', 'E', 'C', 'C', 'C', 'A', 'C', 'D', 'E', 'C', 'C', 'D', 'B', 'C', 'E', 'E', 'C', 'A', 'D', 'D', 'C', 'C', 'A', 'C', 'C', 'C', 'D', 'C', 'D', 'D', 'C', 'C', 'C', 'B', 'C', 'B', 'E', 'C', 'C', 'B', 'E', 'E', 'C', 'E', 'C', 'E', 'C', 'C', 'A', 'E', 'C', 'A', 'E', 'D', 'B', 'D', 'C', 'E', 'C', 'E', 'E', 'E', 'A', 'C', 'D', 'C', 'C', 'C', 'C', 'A', 'C', 'C', 'D', 'E', 'C', 'D', 'E', 'D', 'E', 'E', 'E', 'C', 'E', 'B', 'E', 'C', 'B', 'D', 'B', 'E', 'E', 'C', 'B', 'C', 'A', 'D', 'E', 'C', 'A', 'A', 'D', 'C', 'E', 'C', 'E', 'B', 'E', 'C', 'A', 'B', 'E', 'A', 'C', 'A', 'B', 'C', 'C', 'D', 'E', 'E', 'C', 'D', 'C', 'E', 'D', 'C', 'A', 'C', 'E', 'E', 'D', 'E', 'C', 'B', 'C', 'C', 'C', 'B', 'B', 'C', 'E', 'C', 'D', 'E', 'D', 'E', 'B', 'B', 'C', 'E', 'C']
Q4. Write a function which maps a random sequence as above into its Huffman code and test it.¶
def CodeHuffman(x, codes):
result = ""
for elt in x:
result += codes.get(chr(65 + elt))
return result
compressedMessage = CodeHuffman(message, codes)
print(compressedMessage)
0010110111000001111001110101011111100111100100110000010110010011011101101011011000110011001100001101100101110111011101111100101110011001101000010111111111010010110010110101001011111011110011110011001110111001011011010000101111010101001010111001101001000010100111010100011110000001110010101101110101010111110011001000110101101101111101000110110011011111100110101111010011010111101111101001111001101000010000110000111010011110000101110010111100010100001011010100011111001001011111101110110010101110011010001110111100001011101111100010101111101111101110011110110101010101011101110100000110100011100111110000111111011101111011000111110011110011001100100111011101010101100110111111100110011110101100111101101111100000100111010101111011001101001001010001100100001000100111011101001001011110001110001000101111001011100111111010010110100100000101010110100011001101110011011111101110111001001110100111101110101011101111111111000101000010000101111010111110111111111101111101110110101110111111011001001011110100100101011101111101110100110111100010011000101111111010101111010100011111110111101100001101100111010111110111111011001110
Q5. Compare with the Shannon bound.¶
Let \(A\) be an alphabet, and let \(pa\) for \(a \in A\) denote the probability of occurrence of letter \(a \in A\).
Shannon bound : $\( -\sum_{a \in A}^{}p_a log_2(p_a) \)$
Shannon bound is actually implemented above (ShannonEntropy)
From Kraft’s inequality :
Huffman coding gives an expected length \(L\) per letter satisfying:
\[H(p) ≤ L ≤ H(p) + 1\]
def expectedCodeLength(p, codes):
codeLength = 0
for idx, prob in enumerate(h):
c = codes.get(chr(65 + idx))
codeLength += prob * len(c)
return codeLength
print("Shannon Entropy :", ShannonEntropy(h))
print("Expected code length using Huffman : ", expectedCodeLength(h, codes))
Shannon Entropy : 2.1464393446710153
Expected code length using Huffman : 2.2
Q6. Write below a function that decodes the Huffman code and test it on a random sequence. Check that it is the inverse of the coding map.¶
def DecodeHuffman(code, root):
result = ''
curr = root
for bit in code:
if bit == '1':
curr = curr.right
elif bit == '0':
curr = curr.left
if (curr.left == None and curr.right == None):
result += curr.name
curr = root
return result
print(DecodeHuffman(compressedMessage, root))
CCDDBCCCCEAECDCEECCEAABCCCCDAABECBDDACBCBCBCCCBBCDBECECEBCDBCBCBACCDEEBADADDCADEDECCEABCECECCDDDCCCCDECDCADCECCBAACCDCCECDCCCEACCCCECCDCBECDCDEABCACBDDDEDCCCBBCBEECCBDECABDECEBAEABACCACCBCCCECAEACCDBCDECCCDCCCCDDCACEBCADEBECBCDCECCBACECEACCDBEBCCDCEBEBECCEDDCDCDCECECACCCBACECCEBCCCEECECEDACEBCEABCBCAECECDCDABEEABCEDCBCEDDEACCCAECDCEDABAADCCCBCACCACAECECAADECCCECCCACDECCDBCEECADDCCACCCDCDDCCCBCBECCBEECECECCAECAEDBDCECEEEACDCCCCACCDECDEDEEECEBECBDBEECBCADECAADCECEBECABEACABCCDEECDCEDCACEEDECBCCCBBCECDEDEBBCEC
Block Huffman coding to reach better performances.¶
We consider a probability as below on an alphabet of two letters \(a,b\).
Q7: Compute the entropy associated with this probability and generalize for an alphabet described by blocks of \(k\) letters.¶
t = .12
h = [t, 1-t]
n = 20000
x = (np.random.rand(n) > t) + 1 # Message to encored formed with only 1 and 2 (A and B)
import itertools
# h array of proba
# dim the dimension of the blocks to generate
def CreateBlockTree(h, dim):
elements = zip(h, range(len(h)))
couples = list(itertools.product(elements, repeat=dim)) # Cartesian product to get all possible couples
# Merge proba of each couple
block = []
keys = []
for couple in couples:
prob = 1
value = ''
for elt in couple:
prob *= elt[0]
value += chr(65 + elt[1])
block.append((prob, value))
keys.append(value)
# Build tree
nodes = [NodeTree(b[1], b[0]) for b in block]
nodes = sorted(nodes, key=lambda node: node.proba, reverse=True)
while (len(nodes) > 1):
left = nodes.pop()
right = nodes.pop()
node = NodeTree('', left.proba + right.proba, left, right)
nodes.append(node)
nodes = sorted(nodes, key=lambda node: node.proba, reverse=True)
return nodes[0], keys
blockRoot, blockKeys = CreateBlockTree(h, 2)
print2DUtil(blockRoot)
BB (0.7744)
(1.0)
BA (0.1056)
(0.12)
AA (0.0144)
(0.2256)
AB (0.1056)
def HuffmanBlockGencode(root, keys):
codes = {}
for i, key in enumerate(keys):
path = []
getPathFromX(root, path, key)
pathChain = ''
for d in path:
pathChain += str(d)
codes.update({keys[i]:pathChain})
return codes
# vector to store the path
blockCodes = HuffmanBlockGencode(blockRoot, blockKeys)
print(blockCodes)
def expectedBlockCodeLength(h, codes):
result = 0
for idx, prob in enumerate(h):
c = codes.get(chr(65 + idx) + chr(65 + idx))
result += prob * len(c)
return result
{'AA': '010', 'AB': '00', 'BA': '110', 'BB': '1'}
Q7bis. Compare the length of the Huffman code and the Shannon bound. How to explain the difference ? In order to improve the result, we use Huffman coding on blocks of length \(k\).¶
print("Expected block code length using Huffman : :", expectedBlockCodeLength(h, blockCodes))
print("Shannon Entropy :", ShannonEntropy(h))
Expected block code length using Huffman : : 1.24
Shannon Entropy : 0.5293608652873644
We have two symbols that needs to be coded on 1 bit. The probabilities of symbol appearance are different than the one of obtain a letter. That is why we are so far from the entropy.
Q8. Write a code that takes as input a sequence of length \(k\) of letters and associate a binary code. Then, write a function that takes as inputs a random sequence its code by block of length \(k\). We assume that the length is a multiple of \(k\).¶
def CodeBlocks(x, codes):
result = ""
for i in range(0, len(x) - 1):
elt = chr(64 + x[i]) + chr(64 + x[i+1]) # AB, BA, AA or BB
result += codes.get(elt)
return result
def GenNewCode(x):
return 0
compressedBlockMessage = CodeBlocks(x, blockCodes)
print(compressedBlockMessage[:512]) # Only print the starts
00111111111111111111110001110010001111111111000111111111111000111111111111110001100011111111111100011111111111111111111111111111111100011111111111111111100011000111111111000111100011111111111111111111110001111111111100011111111111110001110001111111111111111111100011111111111111111111111111111000111001000111111001000111111110001111111111111000111111111111111110001111111111111100011111111111111000111110001100011111111111110001111111100011111111111111000111110001111111111110001111111100011000111001000111111110
Q9. Write a function that gives the empirical probability of the message encoded by \(k\)-blocks.¶
def EstimateProbabilites(codes,blockSize):
return 0
